Answer Set Programming (ASP) mit Clingo

Einleitung

Answer Set Programming (ASP) ist ein deklaratives Programmierparadigma, das auf logischem Schließen basiert. Es eignet sich besonders für kombinatorische Suchprobleme, bei denen man nach Lösungen sucht, die bestimmte logische Bedingungen erfüllen. Clingo, entwickelt von der Universität Potsdam, ist ein leistungsfähiges Werkzeug für ASP, das die Solver Clasp und Gringo kombiniert. Es ermöglicht die Modellierung komplexer Probleme durch präzise logische Regeln und liefert stabile Modelle (Answer Sets) als Lösungen. Dieser Artikel führt in die Grundlagen von ASP mit Clingo ein, zeigt einfache Beispiele inklusive Ausgaben und demonstriert die Flexibilität von Clingo durch Optimierungsprobleme.

Grundlagen von ASP und Clingo

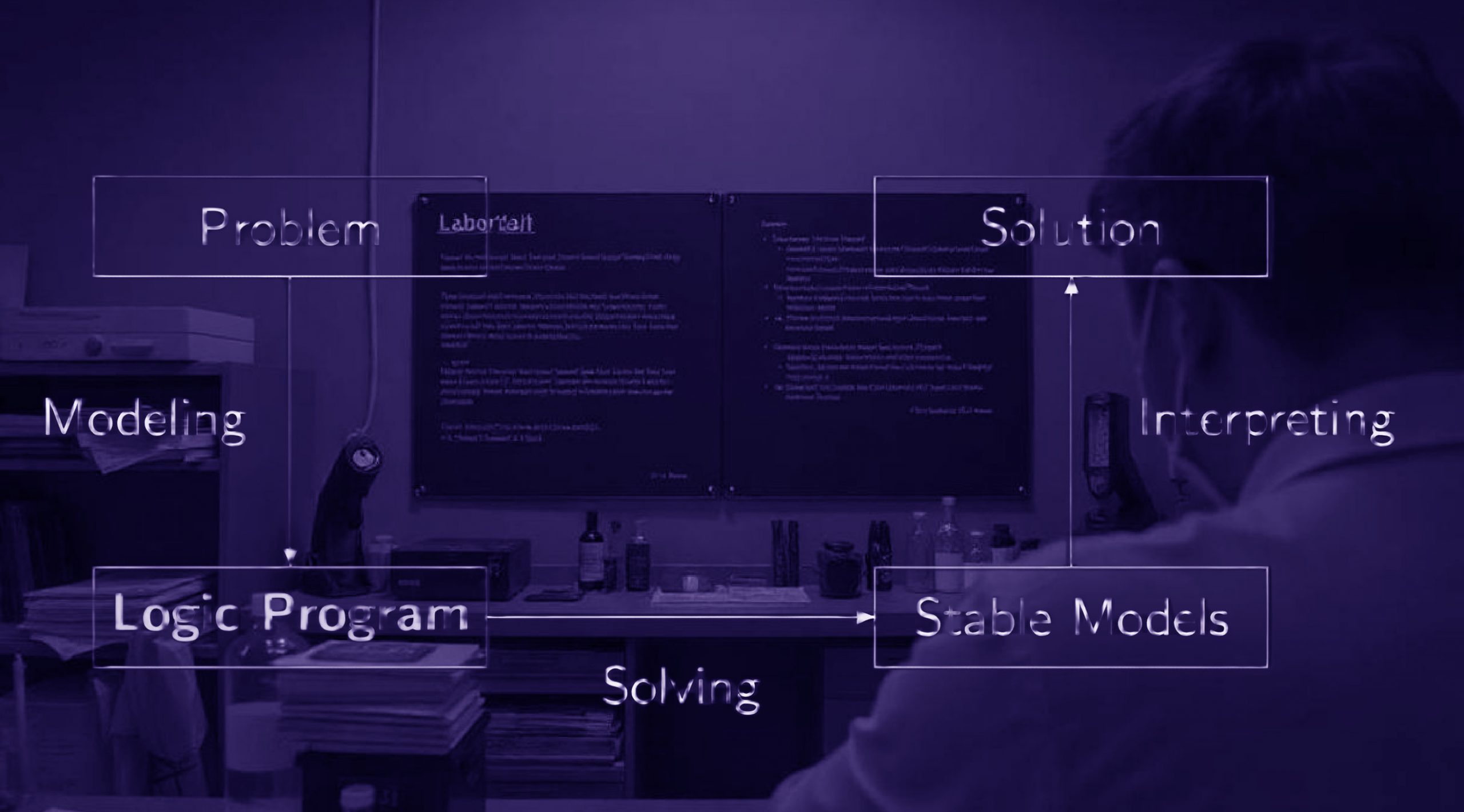
ASP basiert auf der Idee, ein Problem durch eine Menge von logischen Regeln zu beschreiben, die in einem Programm ausgedrückt werden. Ein Answer Set ist eine konsistente Zuweisung von Wahrheitswerten an Prädikate, die alle Regeln des Programms erfüllt. Clingo verarbeitet diese Programme und berechnet die Answer Sets effizient.

Ein typisches ASP-Programm besteht aus:

• Fakten: Direkte Aussagen, z. B. a.
• Regeln: Logische Implikationen, z. B. b :- a. (b ist wahr, wenn a wahr ist)
• Constraints: Bedingungen, die erfüllt sein müssen, z. B. :- a, not b. (a und nicht b dürfen nicht gleichzeitig wahr sein)
• Optimierung: Minimierung oder Maximierung bestimmter Kriterien

Clingo ist flexibel, da es Probleme aus verschiedenen Domänen wie Planung, Scheduling, Konfigurationsproblemen oder Optimierung lösen kann, ohne dass der Benutzer die Suchalgorithmen selbst implementieren muss.

Installation und Ausführung

Clingo kann von der offiziellen Webseite (https://potassco.org/clingo/) heruntergeladen werden. Nach der Installation kann ein ASP-Programm in einer Datei (z. B. program.lp) gespeichert und mit dem Befehl clingo program.lp ausgeführt werden. Clingo gibt die stabilen Modelle (Answer Sets) aus.

Beispiel 1: Färbungsproblem

Ein klassisches kombinatorisches Problem ist die Graphfärbung: Jeder Knoten eines Graphen soll eine Farbe erhalten, sodass benachbarte Knoten unterschiedliche Farben haben.

Programm (graph_coloring.lp):

% Fakten: Knoten und Kanten
node(a). node(b). node(c).
edge(a,b). edge(b,c). edge(c,a).

% Mögliche Farben
color(red). color(blue). color(green).

% Jeder Knoten erhält genau eine Farbe
{ assign(N,C) : color(C) } = 1 :- node(N).

% Benachbarte Knoten dürfen nicht die gleiche Farbe haben
:- edge(X,Y), assign(X,C), assign(Y,C).

Erklärung:

• node/1 und edge/2 definieren den Graphen (ein Dreieck).
• color/1 definiert die verfügbaren Farben.
• Die Regel { assign(N,C) : color(C) } = 1 stellt sicher, dass jeder Knoten genau eine Farbe erhält.
• Der Constraint :- edge(X,Y), assign(X,C), assign(Y,C). verbietet, dass benachbarte Knoten die gleiche Farbe haben.

Ausführung:

clingo graph_coloring.lp

Beispielausgabe:

Answer: 1
assign(a,red) assign(b,blue) assign(c,green)
Answer: 2
assign(a,blue) assign(b,red) assign(c,green)
...
SATISFIABLE

Clingo findet alle möglichen Färbungen, z. B. Knoten a rot, b blau, c grün. Dies zeigt, wie Clingo kombinatorische Probleme effizient löst.

Beispiel 2: Planungsproblem

Ein weiteres Beispiel ist die Planung von Aufgaben. Angenommen, wir haben drei Aufgaben (t1, t2, t3), die in zwei Zeitschlitzen (1, 2) ausgeführt werden sollen, wobei manche Aufgaben nicht gleichzeitig ausgeführt werden dürfen.

Programm (scheduling.lp):

% Fakten: Aufgaben und Zeitschlitze
task(t1). task(t2). task(t3).
slot(1). slot(2).

% Jede Aufgabe wird genau einem Zeitschlitz zugewiesen
{ schedule(T,S) : slot(S) } = 1 :- task(T).

% Aufgabe t1 und t2 dürfen nicht im gleichen Zeitschlitz sein
:- schedule(t1,S), schedule(t2,S).

Erklärung:

• task/1 und slot/1 definieren Aufgaben und Zeitschlitze.
• { schedule(T,S) : slot(S) } = 1 weist jeder Aufgabe genau einen Zeitschlitz zu.
• Der Constraint verhindert, dass t1 und t2 im gleichen Zeitschlitz geplant werden.

Ausführung:

clingo scheduling.lp

Beispielausgabe:

Answer: 1
schedule(t1,1) schedule(t2,2) schedule(t3,1)
Answer: 2
schedule(t1,2) schedule(t2,1) schedule(t3,1)
...
SATISFIABLE

Dies zeigt, wie Clingo Planungsprobleme löst, indem es alle möglichen Zuweisungen findet, die die Bedingungen erfüllen.

Beispiel 3: Optimierungsproblem

Clingo kann auch Optimierungsprobleme lösen, z. B. die Minimierung von Kosten. Nehmen wir an, wir haben Produkte mit unterschiedlichen Kosten, und wir wollen eine Auswahl treffen, die bestimmte Bedingungen erfüllt und die Gesamtkosten minimiert.

Programm (optimization.lp):

% Produkte und ihre Kosten
product(p1,10). product(p2,20). product(p3,15).

% Mindestens zwei Produkte auswählen
{ select(P) : product(P,_) } >= 2.

% Kosten berechnen
cost(C) :- C = #sum{ Cost,P : select(P), product(P,Cost) }.

% Minimierung der Kosten
#minimize { Cost,P : select(P), product(P,Cost) }.

Erklärung:

• product/2 definiert Produkte und deren Kosten.
• { select(P) : product(P,_) } >= 2 stellt sicher, dass mindestens zwei Produkte ausgewählt werden.
• #minimize minimiert die Summe der Kosten der ausgewählten Produkte.

Ausführung:

clingo optimization.lp

Beispielausgabe:

Answer: 1
select(p1) select(p3) cost(25)
OPTIMUM FOUND

Clingo wählt p1 (Kosten 10) und p3 (Kosten 15), da dies die kostengünstigste Kombination ist, die die Bedingung (mindestens zwei Produkte) erfüllt.

Flexibilität von Clingo

Die Beispiele zeigen, wie flexibel Clingo ist:

• Graphfärbung: Kombinatorische Probleme mit Constraints.
• Planung: Zuweisungsprobleme mit zeitlichen oder ressourcenbasierten Einschränkungen.
• Optimierung: Minimierung oder Maximierung von Kriterien wie Kosten oder Ressourcen.

Clingo kann auch komplexere Probleme wie Sudoku, Scheduling in der Produktion, Konfigurationsprobleme in der Softwareentwicklung oder sogar KI-Planungsaufgaben lösen. Durch die deklarative Natur von ASP müssen Benutzer nur das Problem modellieren, während Clingo die Suche nach Lösungen übernimmt. Die Unterstützung für Optimierung, Constraints und die Möglichkeit, große Programme zu verarbeiten, macht Clingo zu einem mächtigen Werkzeug.

Fazit

Answer Set Programming mit Clingo bietet eine elegante Möglichkeit, komplexe kombinatorische und Optimierungsprobleme zu lösen. Die deklarative Modellierung erlaubt es, Probleme präzise zu beschreiben, ohne sich um die Implementierung von Suchalgorithmen kümmern zu müssen. Die vorgestellten Beispiele – Graphfärbung, Planung und Kostenminimierung – verdeutlichen, wie vielseitig Clingo ist. Durch die einfache Syntax und die leistungsstarken Solver-Funktionen eignet sich Clingo sowohl für akademische Forschung als auch für industrielle Anwendungen.

Weiterführende Ressourcen:

• Offizielle Clingo-Dokumentation: https://potassco.org/clingo/
• ASP-Tutorials: https://potassco.org/doc/

Dieser Artikel bietet einen Einstieg in ASP mit Clingo und zeigt, wie einfach es ist, komplexe Probleme zu modellieren und zu lösen. Mit Clingo können Entwickler und Forscher eine Vielzahl von Anwendungen effizient umsetzen.